Quick Start¶

This is a quick start tutorial, containing code snippets to show Tuun usage.

Minimal example¶

Here is a minimal working example, which uses Tuun to optimize a function via Bayesian optimization. Tuun is instantiated, a search space is specified (a one-dimensional continuous Euclidean space within $[-5, 5]$ ), a function is defined, and Tuun’s minimize_function is called.

from tuun.main import Tuun

# instantiate Tuun
tu = Tuun()

# set search space
search_space = ('real', [-5, 5])
tu.set_config_from_list(search_space)

# define function to optimize
f = lambda x: x[0] ** 4 - x[0] ** 2 + 0.1 * x[0]

# minimize function over search space
result = tu.minimize_function(f, 20)

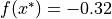This should find a minima at roughly: $x^* = [ -0.73 ]$ , where $f(x^*) = -0.32$ . For details on specifying the search space, see this page.

Additional options¶

Tuun also allows for fine-grained configuration of individual components and search spaces.

from tuun.main import Tuun

config = {
    # configure tuning backend
    'backend': 'probo',

    # configure model
    'model_config': {'name': 'simplegp', 'ls': 3.0, 'alpha': 1.5, 'sigma': 1e-5},

    # configure acquisition function
    'acqfunction_config': {'name': 'default', 'acq_str': 'ei'},

    # configure acquisition optimizer
    'acqoptimizer_config': {'name': 'default', 'max_iter': 200},

    # configure domain
    'domain_config': ('real', [-5, 5]),
}
tu = Tuun(config)

f = lambda x: x[0] ** 4 - x[0] ** 2 + 0.1 * x[0]
result = tu.minimize_function(f, 20)

For details on configuring components, see this page, and for details on specifying the search space, see this page.

Initialize with a dataset¶

We often want to start optimization with an initial dataset of 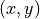$(x, y)$ pairs. The script below shows how to initialize Tuun with a given dataset. In this case, we initialize with a dataset of 3 function queries.

from tuun.main import Tuun

# instantiate Tuun
tu = Tuun()

# set search space
search_space = ('real', [-5, 5])
tu.set_config_from_list(search_space)

# define function to optimize
f = lambda x: x[0] ** 4 - x[0] ** 2 + 0.1 * x[0]

# set initial dataset
data = {'x': [[0.0], [1.0], [2.0]], 'y': [6.0, 3.0, 4.0]}

# minimize function over search space
result = tu.minimize_function(f, 20, data=data)